4Ming Kurve
Die von uns entwickelte 4Ming-Kurve, basierend auf der mathematischen Superellipse (Lame-Kurve), optimiert den Tiefziehprozess durch die Vermeidung typischer Krümmungssprünge am Ziehkanteneinlauf und -auslauf. Diese geometrische Anpassung führt zu einer gleichmäßigen Spannungsverteilung und eliminiert lokale Spannungskonzentrationen, die beim traditionellen Ziehradius auftreten.
In praktischen Anwendungen, wie der Umformung eines Edelstahlbehälters, konnte ein signifikant höheres Ziehverhältnis erreicht werden, während gleichzeitig die erforderliche Ziehkraft reduziert und Schmierstoffe mit geringerer Scherfestigkeit verwendet werden können.
Die gleichmäßige Spannungsverteilung führt zu einer signifikanten Verringerung der Verschleißmechanismen Adhäsion und Abrasion. Dies ist insbesondere für Werkzeugwerkstoffe mit geringer Druckfestigkeit (z.B. Zamak) interessant.
Es wurden von uns mehrere Tiefziehwerkzeuge mit der 4Ming Kurve ausgeführt. Zusammenfassend können wir folgende Vorteile nachweisen:
- Steigerung des Ziehverhältnis
- Verringerung der Stempelkraft
- Verringerte Schädigung der Ziehkurve
- Verbesserte Reibungsverhältnisse
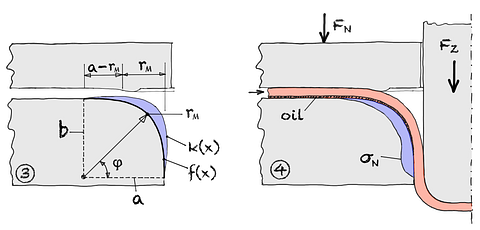
Spannungsverteilung am klassischen Ziehradius
Am Ziehkanteneinlauf und -auslauf kommt es aufgrund der geometrischen Krümmungssprünge zu Normalspannungsmaxima σN. Diese führen zu einer lokalen Konzentration der Normalspannungen σN infolge der Biege- und Rückbiegemomente. Die hohen Normalspannungen bewirken, dass sich Schmierstoff vor der Umformzone aufstaut und abgequetscht wird, was den Einsatz von Ölen mit hoher Scherfestigkeit erforderlich macht (siehe Stribeck-Kurve).

4Ming Kurve
Die von uns entwickelte 4Ming-Kurve basiert auf der sogenannten Superellipse (mathematisch: Lame-Kurve f(x) ). Dadurch werden die typischen Krümmungssprünge am Ziehkanteneinlauf und -auslauf vermieden. Die Krümmung k(x) erreicht an einer definierten Stelle ein Maximum, wobei der minimale Krümmungsradius rmin genau dem klassischen Ziehradius rm entspricht.
Das typisch abquetschen von Öl am Ziehringeinlauf wird verhindert. Es können Öle mit geringer Scherfestigkeit eingesetzt werden. Es sind höhere Ziehverhältnisse erreichbar und typische Verschleißerscheinungen am Werkzeug oder Blech werden herabgesetzt.
Superellipse
Die Superellipse ist eine geometrische Figur, die eine Erweiterung der Ellipse darstellt und durch die Gleichung 1 definiert wird. In dieser Gleichung sind a, b und n die Hauptparameter, die die Form und Ausdehnung der Superellipse bestimmen. Der Parameter a beschreibt die Halbachse entlang der x-Achse, während b die Halbachse entlang der y-Achse angibt. Der Parameter n beeinflusst die Rundung der Kurven, bei n = 2 erhält man eine Ellipse, während größere Werte von n zu schärferen Ecken und kleinere Werte zu weicheren, mehr kreisähnlichen Formen führen. Die Superellipse ist vielseitig in der Gestaltung und findet Anwendungen in Bereichen wie Architektur und Industriedesign.
DIe Krümmung k(x) der Superellipse beginnt und endet bei 0, dazwischen gibt es ein Maximum max( k(x) ) . k(x) kann durch folgenden Zusammenhang algebraisch hergeleitet werden:
Das Krümmungsmaximum max( k(x) ) erhält man, indem man die Ableitung von k(x) gleich null setzt. Diese Gleichung 3 ist transzendent und kann nicht nach x aufgelöst werden. Zur Ermittlung von max( k(x) ) kommt mit der Methode des Goldenen Schnitts ein numerisches Näherungsverfahren zum Einsatz.
Beispiele
