Matrizenradius
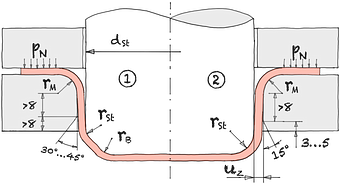
Beim Durchlaufen des Ziehkantenradius rM erlebt das Blech tangentialen Druck aufgrund der Verringerung des Durchmessers. Diese Druckspannungen werden von indirekten Zugspannungen überlagert, die durch den Ziehstempel über den Rand in den Umformbereich übertragen werden. Ein überdimensionierter Matrizenradius kann Falten im Material verursachen.
Zudem tritt beim Durchlaufen eine Biegung und Rückbiegung des Bleches auf. Der Ziehkantenradius erzeugt dabei Bereiche mit variierenden Kontaktnormalspannungen.
Ein zu eng gewählter Ziehkantenradius kann den Fluss des Blechmaterials stören, was zu Rissen im Bodenbereich führen kann.
| Matrizenradius | rM | = | mm |
| Konstante | C | = | ||||
| Blechstärke | s0 | = | mm |
| Matrizenradius Folgezüge | rM n | = | mm |
| Konstante | C | = | ||||
| Matrizenradius Vorzug | rM n-1 | = | mm |
Laut Oehler* führt ein zu kleiner Ziehkantenhalbmesser zu Bodenreißern. Zu große Matrizenradien erleichtern eine unerwünschte Faltenbildung, wodurch es zu Verklemmungen im Ziehspalt, Faltenverplättungen und zu Zargenrissen kommt.
| Matrizenradius | rM | = | mm |
| Durchmesser Platine | d0 | = | mm | |||
| Durchmesser Stempel | d1 | = | mm | |||
| Grenzziehverhältnis | β100 | = | ||||
| Blechstärke | s0 | = | mm |
Die empirisch festgelegten Faktoren 0,04 und 50 basieren auf der Erfahrung, dass bei Werkzeugen mit geringen Standmengen die erforderliche Nacharbeit durch Abrieb, Riefen und Aufschweißungen zu einer fortlaufenden Vergrößerung von rM führt.
Hier gilt die Regel: 5 < rM / s0 < 10 da gemäß Biegeanteil ab rM / s0 > 5 keine Blechdickenminderung und bei rM / s0 < 10 kein Abheben des Bleches von der Ziehkante unter Einwirkung tangentialer Stauchspannungen mehr eintritt.
Dies steht oft im Zusammenhang mit zu geringer Niederhalterpressung oder Blechhalter-Auffederung. Durchbiegung von Pressentisch und Spannelementen führt zu Quetschfalten und raschem Werkzeugverschleiß.
Zu große Ziehkantenradien können nicht verkleinern werden. Zu kleine Ziehkantenradien, ob gewollt oder ungewollt, nehmen zu. Eine beabsichtigte Standmengenerhöhung durch Oberflächenbehandlung und Beschichtungsverfahren muss speziell diesen Bereich fehlerfrei erfassen.*
| Matrizenradius | rM | = | mm |
| Durchmesser Platine | d0 | = | mm | |||
| Durchmesser Stempel | d1 | = | mm | |||
| Blechstärke | s0 | = | mm |
Zwischen dem optimalem Ziehkantenradius und der Blechdicke besteht ein quadratischer Zusammenhang.* Die Blechdicke beeinflusst dabei maßgeblich die Biegekraft. Zwischen Biegekraft am Ziehkantenradius und Blechdicke besteht ebenfalls ein quadratischer Zusammenhang.
| Optimaler Ziehkantenradius | rM opt | = | mm |
| Reibwert | μ | = | ||||
| Dehngrenze | Rp 0,2 | = | MPa | |||
| Blechstärke | s0 | = | mm |
Diese Beziehung gilt für:
- Stahlblech DC04, DC04ZE, ZstE340ZE, ZstE250i, Zst300BH
- Aluminiumblech AA5182-0, AA6009-T4, AA6016-T4
Mit den Eigenschaften:
- μ = 0,02 … 0,15
- s0 = 0,7 … 1,5
- RP 0,2 = 150 … 350 MPa
Werkstoffkennwerte z.B. aus der Tabelle für Beispielwerkstoffe.
Reibwerte siehe Reibwerttabelle oder Reibung & Tribologie.
| Ziehkantenradius Aluminium | rM max Alu | ≤ | mm |
| Blechstärke | s0 | = | mm |
Der maximale Ziehkantenradius für Aluminium wird von Haller* abgeschätzt. Der Ziehradius rM max Alu sollte so groß wie möglich gewählt werden. Dabei zeigt sich, dass ab einem relativen Ziehkantenradius rz / so ≤ 16 der Kraftbedarf nicht mehr signifikant vermindert wird.
| Matrizenradius | rM | = | mm |
| Konstante | C | = | ||||
| Durchmesser Platine | d0 | = | mm | |||
| Durchmesser Stempel | d1 | = | mm | |||
| Blechstärke | s0 | = | mm |
Die so ermittelten Werte können nach* um 20 % gemindert werden, wenn
- das Ziehteil einen Flansch behält oder
- das Ziehverhältnis β1 < 1,4 ist