App loading...
5
Runde Ziehteile
5.1
Umformgrade Tiefziehen
203 Artikel  2254 Elemente

Umformgrade Tiefziehen

5.1
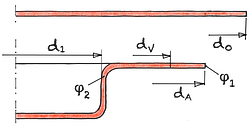
Umformgrade
Abb. 1
Ermittlung der Umformgrade φ1 und φ2
d1 Durchmesser Stempel dV Verglechsdurchmesser, dA Durchmesser Flansch d0 Durchmesser Platine

Wird das Ziehteil mit einem verbleibenden Flansch gezogen, lassen sich die Umformgrade durch folgende Vorgehensweise bestimmen:

  1. Berechnung des Umformgrades an der Außenzone dA
  2. Berechnung eines virtuellen Durchmessers dV durch Volumengleichheit
  3. Berechnung des Umformgrades an der Innenzone d1
  4. Substitution von dV

Beim Tiefziehprozess wird der Durchmesser der Platine d0 auf den Außendurchmesser des Flansches dA verkleinert. Parallel dazu wird ein innerer "virtueller" Durchmesser dV auf den Stempeldurchmesser d1 reduziert. Der virtuelle Durchmesser dV ist genau jener Durchmesser, bei dem zwischen den Volumenanteilen von dA zu dV und von dV zu d1 eine Volumenkonstanz erreicht wird.9

Der "virtuelle" Durchmesser dV kann daher durch folgende Gleichung ermittelt werden:

Gl. 1
\require{color}\definecolor{myred}{RGB}{255,0,0} d_{\color{myred}0}^{\color{myred}2}-d_{\color{myred}A}^{\color{myred}2}={d^{\color{myred}2}}_{\color{myred}V}-d_{\color{myred}1}^{\color{myred}2}\Rightarrow d_{\color{myred}V}=\sqrt{d_{\color{myred}0}^{\color{myred}2}-d_{\color{myred}A}^{\color{myred}2}+d_{\color{myred}1}^{\color{myred}2}}
Gl. 2
\require{color}\definecolor{myred}{RGB}{255,0,0} \varphi_{\color{myred}1}=\beta_{\color{myred}a}=\ln\left(\frac{d_{\color{myred}0}}{d_{\color{myred}A}}\right)
Gl. 3
\require{color}\definecolor{myred}{RGB}{255,0,0} \varphi_{\color{myred}2}=\beta_{\color{myred}i}=\ln\left(\frac{d_{\color{myred}V}}{d_{\color{myred}1}}\right)=\ln\left(\frac{\sqrt{d_{\color{myred}0}^{\color{myred}2}-d_{\color{myred}A}^{\color{myred}2}+d_{\color{myred}1}^{\color{myred}2}}}{d_{\color{myred}1}}\right)
Umformgradφ1=0,16 
φ2=0,37 
Durchmesser Platined0 = 200mm
Durchmesser FlanschdA = 170mm
Durchmesser Stempeld1 = 100mm
200
Ber. 1
Umformgrade Tiefziehen9

Für den Durchzug gilt:

Gl. 4
\require{color}\definecolor{myred}{RGB}{255,0,0} d_{\color{myred}A}=d_{\color{myred}1}\Rightarrow\varphi_{\color{myred}1}=\varphi_{\color{myred}2}

Gemäß35 kann der Durchmesser dA max, der beim Maximum der Ziehkraft erreicht wird, mit folgender Gleichung bestimmt werden:

Gl. 5
\require{color}\definecolor{myred}{RGB}{255,0,0} d_{\color{myred}A\;max}=C\cdot d_{\color{myred}0}
Gl. 6
\require{color}\definecolor{myred}{RGB}{255,0,0} C=\sqrt{0,6+\frac{0,4\cdot d_{\color{myred}1}^{\color{myred}2}}{d_{\color{myred}0}^{\color{myred}2}}}
FlanschaußenranddA max=167,33mm 
KonstanteC=0,84 
Durchmesser Platined0 = 200mm
Durchmesser Stempeld1 = 100mm
200
Ber. 2
Flanschdurchmesser Ziehkraftmaximum35
9
Siegert, K. / Blechumformung / Springer Vieweg / Berlin / 2015 / …
35
Strackerjahn, W. / Die Voraussage des Versagensfalls beim Tiefziehen rechteckiger Teile / Dissertation / Hannover / 1982 / …
© 2023 4Ming e.K.
Kdia v1.3.1
4Ming® Prototypen, Werkzeuge, Ziehkissen, Pressen
Unternehmensberatung, Prozessentwicklung & Prozessoptimierung
Interaktives technisches Handbuch zur Blechumformung