App loading...
16
Biegen
16.2
Rückfederung
203 Artikel  2254 Elemente

Rückfederung

16.2

Während des Biegeprozesses ① tritt eine elastisch-plastische Beanspruchung auf. Wenn das Werkstück dann entlastet wird ②, führen die verbleibenden inneren Spannungen im Querschnitt zu einem Rückstellmoment, das dazu führt, dass das Werkstück eine Rückfederung erfährt.

Die elastische Rückfederung ist ein zentrales Phänomen beim Biegen von Werkstücken und spielt eine entscheidende Rolle bei der Planung und Ausführung von Biegeprozessen. Um das angestrebte Endprodukt zu erreichen, ist es unerlässlich, die Auswirkungen der elastischen Rückfederung genau vorherzusagen und entsprechend zu kompensieren. Dies kann entweder durch eine anfänglich übermäßige Biegung oder durch einen angepassten Nachbiegeprozess realisiert werden.

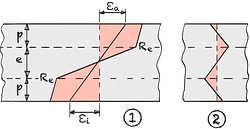
Rückfederung Drehmoment
Abb. 1
Spannungen der Biegezone
① Spannungen unter Last ② Spannungen entlastet
εi Dehnungen Innen εa Dehnungen Aussen e elastischer Bereich p plastischer Bereich Re Streckgrenze

Das Phänomen der Rückfederung ist ein allgegenwärtiger Faktor in sämtlichen Biegeverfahren und muss für eine präzise und fehlerfreie Ausführung des Prozesses berücksichtigt werden. Um eine effektive Kompensation der Rückfederung zu gewährleisten, ist es essenziell, den Rückfederungswinkel oder -radius im Vorfeld genau zu berechnen und in den Biegeprozess einfließen zu lassen.

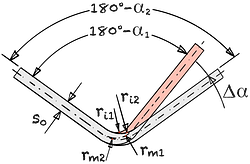
Rückfederung Blech
Abb. 2
Rückfederung Biegen
α1 Biegewinkel unter Last α2 Werkstückwinkel entlastet Δα Rückfederungswinkel rm1 mittlerer Biegeradius unter Last rm2 mittlerer Biegeradius entlastet ri1 Innerer Biegeradius unter Last ri2 Innerer Biegeradius entlastet s0 Blechstärke
Gl. 1
\require{color}\definecolor{myred}{RGB}{255,0,0} k=\frac{\alpha_{\color{myred}2}}{\alpha_{\color{myred}1}}=\frac{r_{\color{myred}m1}}{r_{\color{myred}m2}}=\frac{r_{\color{myred}i1}+0,5\cdot s_{\color{myred}0}}{r_{\color{myred}i2}+0,5\cdot s_{\color{myred}0}}=\frac1{1+3\cdot{\displaystyle\frac{R_{\color{myred}p0,2}}E}\cdot\left(c+{\displaystyle\frac12}\right)}
Gl. 2
\require{color}\definecolor{myred}{RGB}{255,0,0} c=\frac{r_{\color{myred}i2}}{s_{\color{myred}0}}
Gl. 3
\require{color}\definecolor{myred}{RGB}{255,0,0} r_{\color{myred}i1}=k\cdot\left(r_{\color{myred}i2}+0,5\cdot s_{\color{myred}0}\right)-0,5\cdot s_{\color{myred}0}
Gl. 4
\require{color}\definecolor{myred}{RGB}{255,0,0} \alpha_{\color{myred}1}>\alpha_{\color{myred}2}=\frac{\alpha_{\color{myred}2}}k;\;\Delta\alpha=\alpha_{\color{myred}1}-\alpha_{\color{myred}2}
Rückfederungsfaktork=0,981 
Biegefaktorc=5 
Innenradiusri1=4,9mm 
Biegewinkelα1=91,7° 
ÄnderungswinkelΔα=1,697° 
DehngrenzeRp 0,2 = 80MPa
ElastizitätsmodulE = 70GPa
Werkstück-Innenradiusri2 = 5mm
Blechstärkes0 = 1mm
Werkstückwinkelα2 = 90°
80
Ber. 1
Rückfederungsfaktor k nach21
Der Biegefaktor c ist materialspezifisch und darf Mindestwerte nicht unterschreiten.
Werkstoffkennwerte z.B. aus der Tabelle für Beispielwerkstoffe.
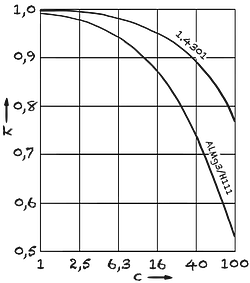
Rückfederung Diagramm
Abb. 3
Rückfederungsfaktor k in Abhängigkeit des Biegefaktors c bei verschiedenen Werkstoffen

Ein längeres Verbleiben des Biegestempels im Biegegesenk ändert nichts am Rückfederungsverhalten. Durch Nachdrücken kann über den Nachschlageffekt eine Reduzierung der Rückfederung erreicht werden.8

8
Oehler; Kaiser / Schnitt-, Stanz- und Ziehwerkzeuge / Springer Verlag / Berlin / 1993 / 7. Auflage
21
Kluge, Siegfried / Prozesse der Blechumformung / Carl Hanser Verlag / München / 2020 / …
© 2023 4Ming e.K.
Kdia v1.3.1
4Ming® Prototypen, Werkzeuge, Ziehkissen, Pressen
Unternehmensberatung, Prozessentwicklung & Prozessoptimierung
Interaktives technisches Handbuch zur Blechumformung